Methodology#
The SIMUnet framework#
The \(\text{SIMUnet}\) methodology [Iranipour and Ubiali, 2022] is an open-source methodology to perform simultaneous PDF-EFT fits and fixed-PDF EFT fits.
It extends the \(\text{NNPDF}\) framework [Ball and others, 2021, Ball and others, 2022] to account for the EFT dependence of the theory cross-sections entering the PDF determination.
This is achieved by adding an extra layer to the \(\text{NNPDF}\) neural network to encapsulate the dependence of the theory predictions on the EFT coefficients, including the free parameters in the general optimisation procedure. This results in a simultaneous fit of the PDF as well as EFT coefficients to the input data.
As in the NNPDF methodology, the error uncertainty estimation makes use of the Monte Carlo replica method, which yields an uncertainty estimate on both PDF and EFT parameters.
The SM theoretical observables are encoded using interpolation grids, known as FK-tables [Ball and others, 2010, Ball and others, 2013, Bertone et al., 2017], which encode the contribution of both the DGLAP evolution and the hard-scattering matrix elements and interface it with the initial-scale PDFs in a fast and efficient way.
The simultaneous fit is represented as a neural network using the
Tensorflow [Abadi et al., 2015] and
Keras [Chollet and others, 2015] libraries. The architecture is
schematically represented in Fig. 1.
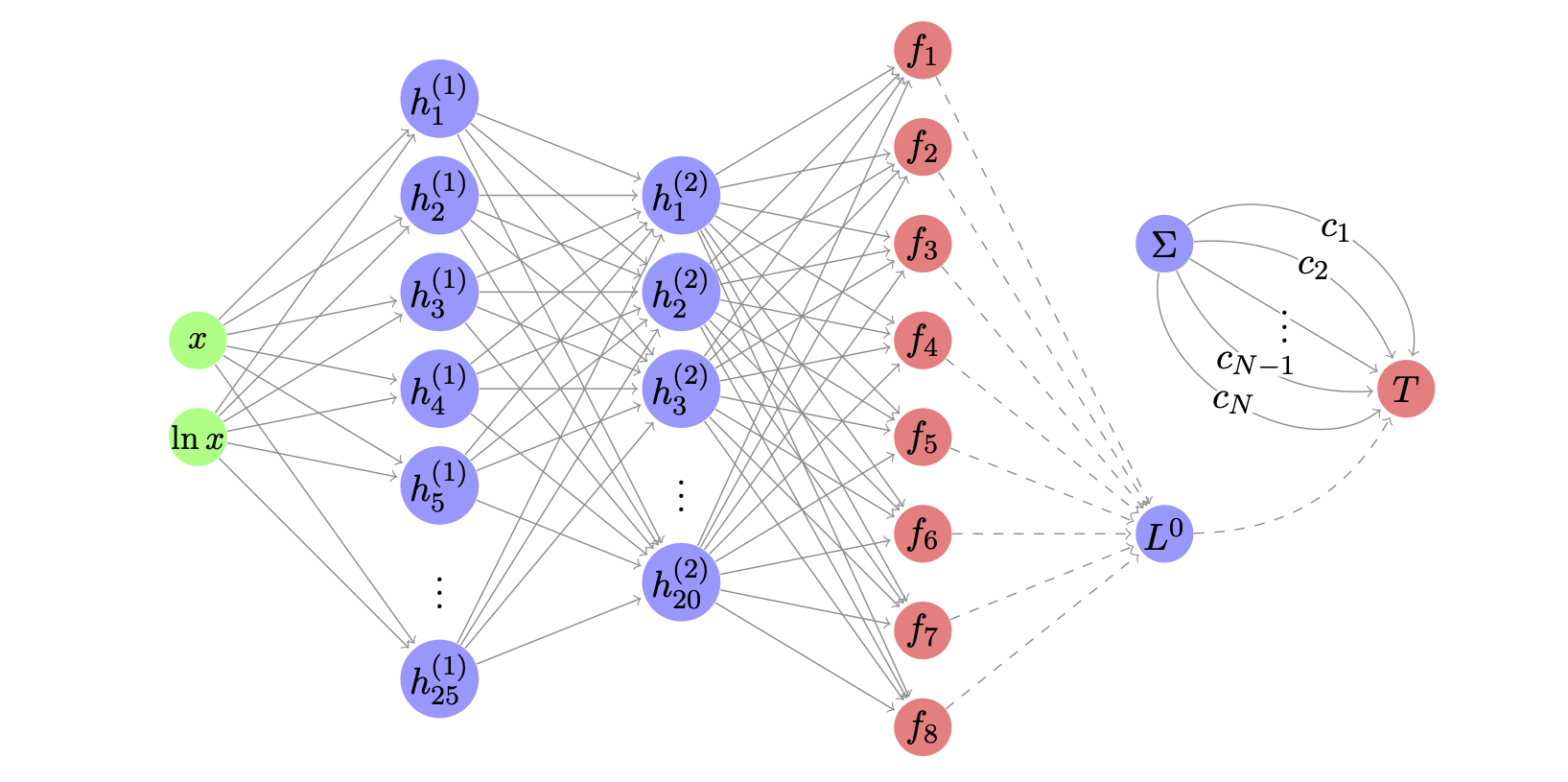
Figure 1: Architecture of the \(\text{SIMUnet}\) methodology.#
In Fig 1., trainable weights are represented by solid arrows, and non-trainable weights by dashed arrows. Through a forward pass across the network, the inputs (\(x\)-Bjorken and its logarithm) proceed through hidden layers to output the eight fitted PDFs at the initial parametrisation scale \(Q_0\).
For each of the experimental observables entering the fit, these PDFs are then combined into a partonic luminosity \(\mathcal{L}^{(0)}\) at \(Q_0\), which is convolved with the precomputed FK-tables \(\Sigma\) to obtain the SM theoretical prediction \(\mathcal{T}^\text{SM}\).
Subsequently, the effects of the \(N\) EFT coefficients \(\boldsymbol{c}=(c_1,\ldots,c_N)\), associated with the operator basis considered, are accounted for by means of an extra layer, resulting in the final prediction for the observable \(\mathcal{T}\) entering the SMEFT-PDF fit.
The \(\text{SIMUnet}\) code allows for linear dependence on the EFT coefficients. In linear EFT fits, the last layer consists of \(N\) trainable weights to account for each Wilson coefficient.
The PDF parameters \(\boldsymbol{\theta}\) and the EFT coefficients \(\boldsymbol{c}\) entering the evaluation of the SMEFT observable in Fig. 1 are then determined simultaneously from the minimisation of the loss function of the fit.
The \(\text{SIMUnet}\) architecture can be minimally modified to deal with the fixed-PDF case, in which only the EFT coefficients of the last layer are treated as free parameters in the optimization process. This can be achieved by freezing the PDF-related weights in the network architecture to the values obtained in some previous fit, for example a SM-PDF determination based on \(\text{NNPDF}\).
In this manner, \(\text{SIMUnet}\) can also be used to carry out traditional EFT fits where the PDF dependence of the theory predictions is neglected.
Furthermore, for PDF-independent observables, computing an FK-table \(\Sigma\) is not required and the SM cross-section \(\mathcal{T}^\text{SM}\) can be evaluated separately and stored to be used in the fit.
As illustrated in Fig. 1, within the \(\text{SIMUnet}\) framework a single neural network encapsulates both the PDF and the EFT dependence of physical observables, with the corresponding parameters being simultaneously constrained from the experimental data included in the fit.
Specifically, we denote the prediction of the neural network as:
with \(n=n_{\rm dat}\) and \(\boldsymbol{\hat{\theta}} = (\boldsymbol{\theta}, \boldsymbol{c})\), where \(\boldsymbol{\theta}\) and \(\boldsymbol{c}=(c_1, \ldots, c_N)\) represent the weights associated to the PDF nodes of the network, and to the \(N\) Wilson coefficients from the operator basis, respectively.
The uncertainty estimation uses the Monte Carlo replica method, where a large number \(N_{\rm rep}\) of replicas \(D^{(k)} = \left( D_1^{(k)}, \ldots, D_n^{(k)} \right)\) of the experimental measurements \(D = \left( D_1, \ldots, D_n \right)\) are sampled from the distribution of experimental uncertainties with \(k = 1, \ldots, N_{\rm rep}\).
The optimal values for the fit parameters \(\boldsymbol{\hat{\theta}}^{(k)}\) associated to each replica are obtained by means of a Stochastic Gradient Descent (SGD) algorithm that minimizes the corresponding figure of merit:
where the covariance matrix in Eq. (1) is the \(t_0\) covariance matrix, which is constructed from all sources of statistical and systematic uncertainties that are made available by the experiments with correlated multiplicative uncertainties treated via the ‘t0’ rescription [Ball and others, 2010] in the fit to avoid fitting bias associated with multiplicative uncertainties.
The \(\text{SIMUnet}\) framework presents a comprehensive and innovative approach to study the PDF-EFT interplay. Its architecture allows for both simultaneous PDF-EFT and fixed-PDF fits, providing flexibility when it comes to assessing their interplay in different sectors. \(\text{SIMUnet}\), combines neural network modeling with advanced statistical methods, ensuring that PDF and EFT coefficients are accurately constrained by experimental data. Additionally, it allows the user to assess if signals of new physics can be absorbed by the PDFs. In this way, \(\text{SIMUnet}\) represents a robust tool for understanding the complex interplay between PDFs and EFT coefficients in high energy physics.
